1. What is Deep Learning & How Does It Work

A brief introduction to deep learning.

Deep Learning in Modern World

If you have a little knowledge about artificial intelligence and machine learning, or if you’re active on social media, you might have heard, “AI will be going to Take over Humanity” or “AI will Take all existing jobs”. Now I’m not here to debate all of these. Instead, I’m going to tell you what makes today’s AI so powerful. The main reason AI is getting better day by day and in some tasks it’s getting better than humans is because of Deep Learning.

Go, is a board game. In this game, an AI named Alpha Go beat the world champion of this game. In recent times if you’re scrolling through Facebook or Twitter you might have seen many posts about AI generating beautiful art. One of the AI that is doing such wonderful art is called Midjourney AI. It can render images from only text input. And the quality of the images is equivalent if not better than that of most artists in modern times. And we can’t forget our personal assistants Google, Alexa, or Siri. We are using these AI for day-to-day usage. All of these AI is possible because of Deep Learning.

Inspiration of Deep Learning

All the advanced AI is made with deep learning. Now, you might want to know 2 things, the first question how does deep learning or neural network actually works, and the second question is what is the inspiration behind deep learning? I will try to answer the second question in this section & in the later section, I will discuss the first question.

The whole concept of deep learning is inspired by the human brain. More specifically the neurons are the main inspiration for deep learning. If you have knowledge of the elementary level of biology then you must be familiar with the term neurons. WHAT? You don’t know what is a neuron? Didn’t pay attention to your biology class in high school? No need to worry. In this section, I’ll be talking about neurons and how it works.

We have neurons all over our bodies. 100 billion neurons only exist in our brains. Yes, you have read that right. It’s billion, not million. The main task of a neuron is to carry information from any part of the body to the brain and carry information from the brain to any part of the body. So, the task is to carry information.

Now, this information is shared by activating neurons. What do I mean by neuron activation? Okay, let’s try to understand from an example. Try to imagine you’re eating yummy food. Now how will the brain know the taste of that food? This taste which is information will go to the brain through neurons. Food taste will activate the neuron inside our mouth and it will carry that information to the brain. Here, only the mouth’s neuron is activated. It didn’t activate another neuron to pass the information.

Neurons don’t only share information with the brain it also helps us means the brain learns new skills or task. How is that? When we’re learning new skills we try to practice that skills a lot. When we’re practicing that particular skill the neuron will try to create a new strong connection with the brain specifically for that skill and that’s how we’re able to learn new skills.

From the above discussion we’re able to know 3 things:

• Neuron carries information.
• Specific neurons get activated for a specific task.
• Training will create a new strong connection between neurons and the brain.

And all of these above were actually the main inspiration to create deep learning.

How Does Deep Learning Work?

Now I will talk about the main topic, which is how does deep learning actually work? We will try to get a high-level overview of the topic. In future articles, I will explain the low-level aspects of deep learning.

Deep learning takes data as input and predicts a value from the data which is the output. This task is done by a neural network. To make our AI expert in a specific task, first, we have to train the neural network with task-related data. After training the neural network becomes an expert in that specific task. There are mainly 2 types of tasks and those are classification tasks & regression tasks.

• Classification Task: Classification tasks are those kinds of tasks where neural networks need to classify 2 or more classes based on the input.

• Regression Task: Regression tasks are those kinds of tasks where neural networks need to predict some continuous values. i.e: what is the height based on the weight of a person, etc.

We can divide the neural networks into 2 portions:

• Neural Network Structure.
• Neural Network Training & Prediction.

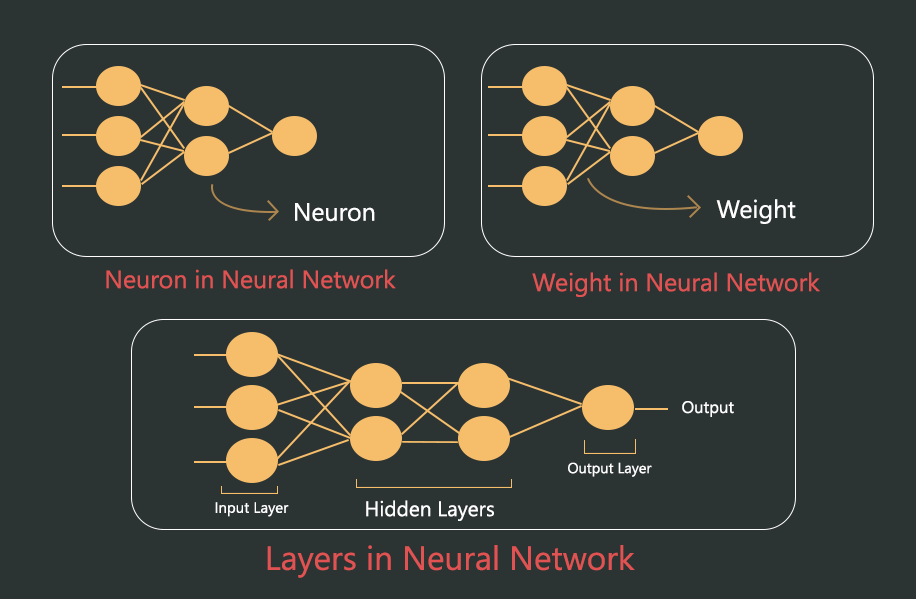
Neural Network Structure

The neural network structure is all the element that creates a neural network. In a neural network structure, there is a total of 3 elements and they are:

1. Neuron
2. Weights
3. Layers
    

 Neuron: Neuron is the unit of the neural network. Neuron store all the information and pass that information to the next layer. Remember in the Inspiration of Deep Learning we discuss that neuron’s main objective is to carry & transfer information. Just like that neurons in neural networks carry information from one layer to the next layer.
 

 Weights: Weights establish the connection between the neurons of two different layers. (We will talk about layers below.) Weights have their own value. This value represents how strongly one neuron is connected to another neuron.
 

 Layers: Above we talked about Layers a lot. Layers are created with the combination of neurons and weights. Each layer has its own neuron and each of the neurons has weights that connect them to the next layer’s neurons. (There is an illustration of the neural network structure below, see the illustration for better clarification) Now in a neural network structure, there are 3 types of layers:
 

  1. Input Layer: This layer takes the input i.e: data. This is the very fast layer in a neural network.
 

  2. Output Layer: The output layer is the last layer in a neural network. This layer gives the output or prediction value.
 

  3.Hidden Layer: Hidden layer is in between the input and output layers. Hidden layers take the input from the input layer and pass the necessary information or values to the output layer. All the calculation for the neural network is computed in the hidden layer.
 

In a neural network, there can only be 1 input or output layer but can have more than 1 hidden layer. The number of hidden layers and the number of neurons needed for each layer is defined based on the problem statement.

Neural Network Training & Prediction

After creating the structure of the neural network next step is to train the neural network for a specific task (classification or regression). Neural network training can be broken down into 3 steps. And those are -

1. Forward Propagation
2. Loss function ( Comparing predicting value with the real value)
3. Backpropagation

All of the steps are executed one after another. Now let’s try to understand what is going on in each step.
 
 

1. Forward propagation:

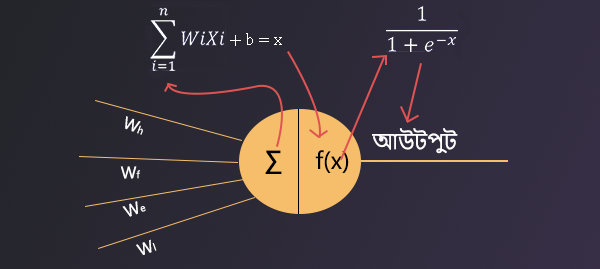
Neural networks make their prediction with forward propagation. In forward propagation, each neuron passes its value to the next layer. One layer’s input is from its previous layer’s output and the output of the current layer is the input of the next layer. And this will continue till the output layer and the output layer will make the final prediction. But now the question is how does the neuron forward the input values to its next layer?Here, each neuron goes through 2 steps in forward propagation to forward the value to the next layer.
 
 

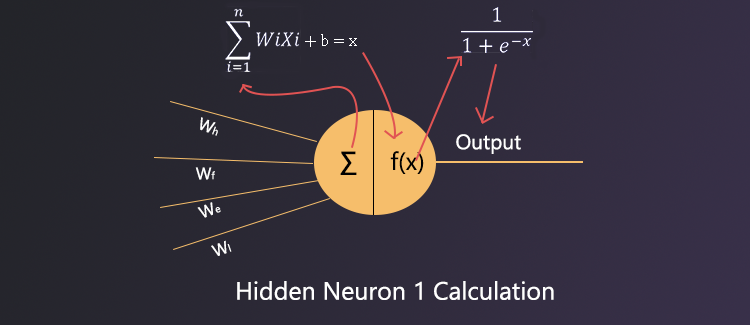
• Weights & Biases : The first step is to calculate the input with the help of weights and biases. Each neuron is connected with all the neurons by individual weights from its previous layer ( See the illustration below for a better understanding). Now all the output of the previous layer is forwarded to the next layer by those weights. Now the inputs (the previous layer’s outputs) & the weights are being calculated inside the neuron itself. Each input is multiplied by the weight it enters through and after multiplying all such inputs and weights, all are added together. In the end, bias is added to the final result. Every neuron has its own bias.

\[x=input \\ w=weight \\ b=bias\] \[ \sum_{i=1}^{n} w_i.x_i+b = w_1.x_1 + w_2.x_2 + \ldots + w_n.x_n + b\]

 

• Activation Function : After calculating the value inside the neuron the value is not directly forwarded to the next layer. Rather it goes through an activation function. In the previous discussion, Inspiration of Deep Learning we discussed the activation of human neurons. Similarly, here activation function decide which neuron will be activated. The activation function takes the calculated value ( in the 1st step) as input and gives an output. This output is forwarded to the next layer. There are many types of activation functions and each serves a different purpose. In the next article, I will write about various types of activation functions.

\[x= \sum_{i=1}^{n} w_i.x_i+b\] $$ f(x) = \frac{\mathrm{1} }{\mathrm{1} + e^- x} $$

f(x) is a sigmoid activation function

2. Loss Function(comparing the predicted value with the original value)

Neural network’s prediction is not enough. We need to verify the prediction. We need to know if the prediction is correct or incorrect. To do this we use the loss function. The loss function compares the predicted output and the original output. If the predicted out and the original output is the same then the loss will be 0. If the predicted output is close to the original output then the loss value would be small but when the predicted output and original output differ then the loss value would be large. By finding out the value of the loss function we are able to know how close is the predicted value to the original value. There are different loss functions for classification and regression tasks.

3. Backpropagation

At the begging of the training, the predicted output of the forward propagation is far from the original output. And it is because at the beginning all the weights have been initialized as 0. If we follow the formula above and we take 0 for every weight then the output would always be 0. So, we can see weight values have a huge impact on the predicted value. If we can find the proper value for each weight then the neural network can make a better prediction that is close to the original output. The neural network needs to update its weight value. But how can it do so? It can update the value of its weights by backpropagation. Backpropagation is a technique where it calculates the error from the original output and predicted output using the loss function. After finding the error it updates all the weights values based on the error. This is a complicated process. There is lots of mathematical operation happening behind the scenes. But for now, I won’t discuss the mathematical parts it’ll be covered in an upcoming article.
 
 

From the above discussion, we find out mainly 3 steps for training a neural network:

• The neural network predicts with the help of forward propagation.
• After predicting, the loss function compares the original and predicted output.
• After computing, the error from the loss function the backward propagation updates each of the weights based on the error value in the loss function.

After completing these 3 steps 1 iteration has been completed. Then neural network starts its 2nd iteration but this time forward propagation is going to use the updated weights. And this iteration will be happening one after another till the error becomes 0 or close to 0.

A Simple Neural Network’s Example

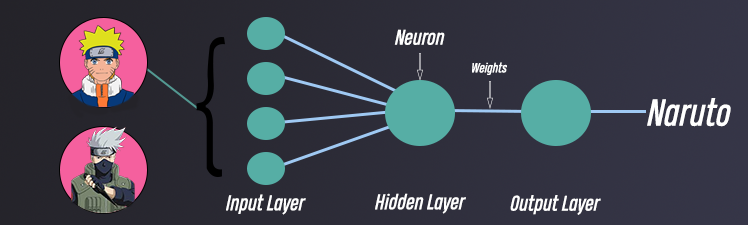
Hey, are you there? I guess that’s a yes. I thought you left when you saw all the math equations. I’m glad that you’re still here and want to learn more. Now let’s go and try to understand a simple example of a neural network. I want to make this example a little bit more interesting. That’s why now we are going to see an example of a neural network that is going to predict one of my favorite anime characters Naruto. We’ll give a picture as input and it’ll predict if the picture is of Naruto or not. This is a binary classification problem.

Creating The Structure of The Neural Network

In the previous section How Does Deep Learning Work? we discussed that the first thing we do is create the architecture or structure of a neural network. In this section, I’ll create the architecture of the neural network for the example. For simplicity, I won’t take the whole picture as input rather only take 4 inputs which are hair, forehead, eyes, and lip from the picture. So, we have 4 inputs that will go to the input layer. After the input layer neural network has hidden layers. This is a simple example that’s why there will be only one neural network and it has only one neuron. After that neural network has an output layer and it has only one neuron ( cause this is a binary classification problem). The hidden layer and the output layer both layer’s will have a sigmoid activation function. The final structure of the network is -

• 4 neurons in the input layer for 4 different inputs
• 1 hidden layer and 1 neuron for the hidden layer
• 1 neuron in the output layer.
• Sigmoid activation function for both hidden and output layer

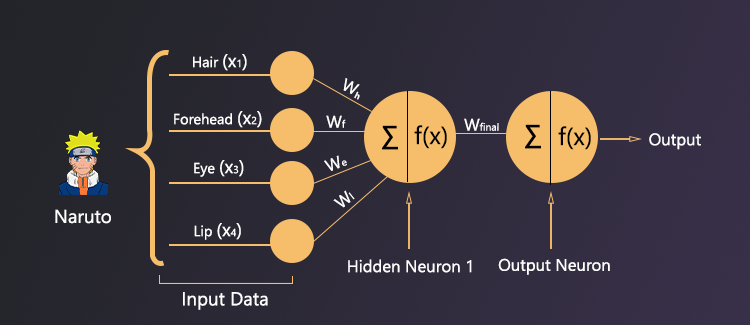
Forward Propagation for 1st Iteration

From the above picture, we can clearly see there are 4 inputs and those are hair, forehead, eye, and lip. And those inputs are connected to the hidden layer’s hidden neuron 1 through W_h, W_f, W_e, W_l all of these weights respectively. And the hidden layer’s hidden neuron 1 is connected to the output layer’s output neuron through W_final weight. This is the first iteration so all the values of weights will be 0. And the bias of the hidden neuron 1 and output neuron 1 will be 0 too. And for simplicity, we will represent the input (hair, lip, etc.) as some constant scaler value. And those values are hair(x1) = 5000, forehead(x2) = 8000, eye(x3) = 2000, lip(x4) = 1000. Now we have to the forward propagation.

 
 

Forward Propagation for Hidden Neuron 1 :

\[x_1 = 5000, x_2=8000, x_3=2000, x_4=1000\] \[w_h=0,w_f=0,w_e=0,w_l=0,b=0\] \[X= \sum_{i=1}^{n} w_i.x_i+b \textrm{ where, n = 4} \] \[X= x_1.w_h + x_2.w_f + x_3.w_e + x_4.w_l+b\] \[X= 5000.0 + 8000.0 + 2000.0 + 1000.0\] \[X= 0\] $$ \textrm{Sigomoid Activation Function Apply} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-X} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-0} $$ $$ f(X) = 0.5 $$ $$ \textrm{Output of hidden neuron1 = 0.5} $$

 
 

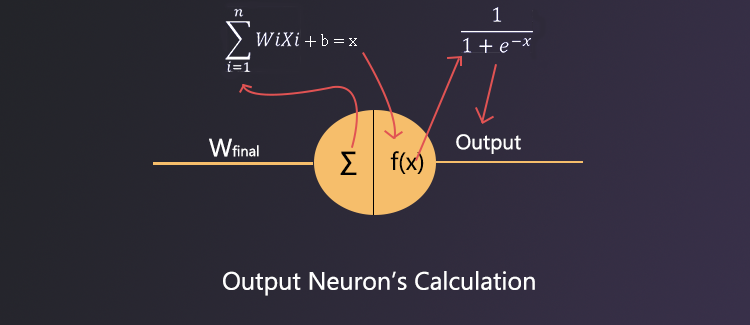
Output Neuron’s Forward Propagation -

Here, the output of hidden neuron 1 (0.5) will be the input of the output neuron. And hidden neuron 1 is connected to output neuron through W_final. Output neuron's bias will be 0 too at first iteration.

\[x_{h1} = 0.5\] \[w_{final}=0,b=0\] \[X= \sum_{i=1}^{n} w_i.x_i+b \textrm{ where, n = 1} \] \[X= x_{h1}.w_{final}+b\] \[X= 0.5*0+0\] \[X= 0\] $$ \textrm{Sigomoid Activation Function Apply} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-X} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-0} $$ $$ f(X) = 0.5 $$ $$ \textrm{Output neuron's Output = 0.5} $$

 
 

Deciding the threshold for output: Here, the neural network’s final output value is 0.5. Now we have to convert this value to yes or no output. To do that we need to set a threshold so that when the value goes above the threshold then it can become 1 which means yes otherwise the final output will be 0 which means no. 0.5 is the threshold for this example. Anything below the threshold will return 0 and anything upper than the threshold will return 1.

\[ \textrm{Output} = \begin{cases} \textrm{Yes} & \text{if $output>0.5$,}\\ \textrm{No} & \text{else $output<=0.5$.} \end{cases} \]

 
 

The final output of the neural network was 0.5 but our threshold is 0.5. So it means neural network predicted no.

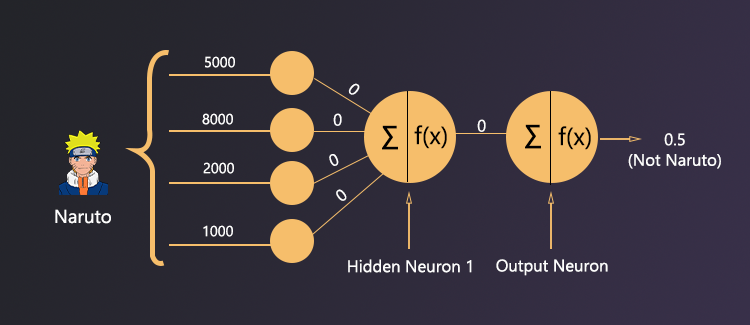
Comparing Predicted Value & Original Output

After the first iteration, the predicted output is no. But the original output was yes. That means the neural network made a wrong prediction. So, now we have to update the weights of hidden neuron 1 and output neuron so that it can make better predictions in the next iteration The loss function will calculate the error between the original and predicted value and then we move on to the next phase which is backpropagation.

Backpropagation

We already know that our prediction is wrong. That means the neural network needs to update the values of the weights. In the backpropagation method, the neural network will update all of its weights based on the error which is calculated by the loss function.

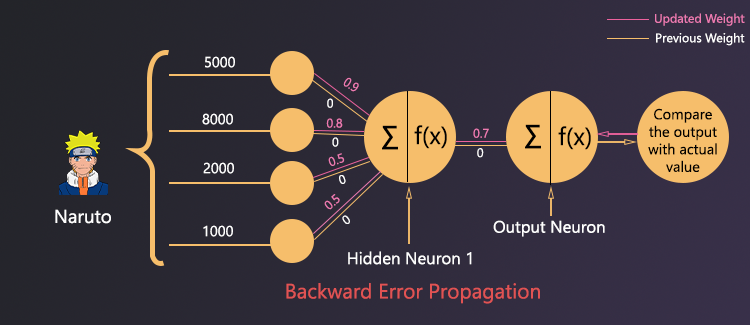
Forward Propagation With Update Weights (2nd Iteration)

After the backpropagation in the 1st iteration, the updated weights are W_h = 0.9, W_f = 0.8, W_e = 0.5, W_l = 0.5

 
  Forward Propagation of Hidden Neuron 1 (after updated weights)

\[x_1 = 5000, x_2=8000, x_3=2000, x_4=1000\] \[w_h=0.9,w_f=0.8,w_e=0.5,w_l=0.5,b=0\] \[X= \sum_{i=1}^{n} w_i.x_i+b \textrm{ where, n = 4} \] \[X= x_1.w_h + x_2.w_f + x_3.w_e + x_4.w_l+b\] \[X= 5000.(0.9) + 8000.(0.8) + 2000.(0.5) + 1000.(0.5)\] \[X= 12400\] $$ \textrm{Sigomoid Activation Function Apply} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-X} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-{12400}} $$ $$ f(X) = 1 $$ $$ \textrm{Output of Hidden Neuron1 = 1} $$
 
  Forward Propagation of the output Neuron (after updated weights) :

Here Input will be 1 (cause hidden neuron 1 output is 1) and updated W_final value is W_final = 0.7

 

\[x_{h1} = 1\] \[w_{final}=0.7,b=0\] \[X= \sum_{i=1}^{n} w_i.x_i+b \textrm{ where, n = 1} \] \[X= x_{h1}.w_{final}+b\] \[X= 0.7*1+0\] \[X= 0.7\] $$ \textrm{Sigomoid Activation Function Apply} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-X} $$ $$ f(X) = \frac{\mathrm{1} }{\mathrm{1} + e^-{0.7}} $$ $$ f(X) = 0.67 $$ $$ \textrm{Output of output Neuron = 0.67} $$

 
 

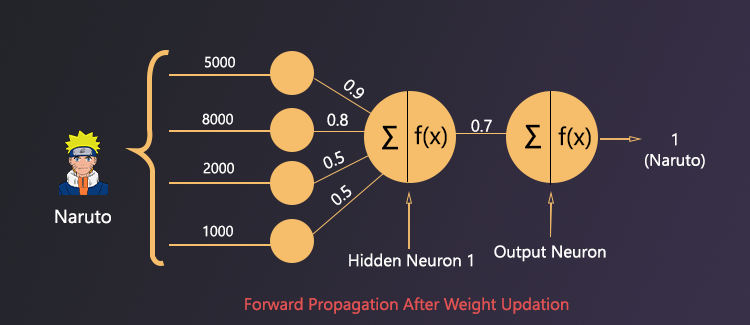
Output Threshold of Our Network :

\[ \textrm{Output} = \begin{cases} \textrm{Yes} & \text{if $output>0.5$,}\\ \textrm{No} & \text{else $output<=0.5$.} \end{cases} \]

 
 

After the 2nd iteration, the output value is 0.67 which is greater than 0.5 then which means the neural network’s final output is yes. This time our neural network can give us the right prediction.

What’s Next?

The above example was a simple example and not something that is practical. Here we trained our neural network with just 1 iteration and with 1 sample image. In real-world scenarios, there will be thousands of samples and we need to train the neural networks for thousands of iterations to update the weights so that we can get an optimal result from the network.
 
  It was a brief introduction to how neural network works. I hope you’ve read so far and at least have basic knowledge of neural networks. This was just the tip of the iceberg, deep learning is a huge topic, and every day this topic is growing at an exponential rate. But still, before diving into the deep of deep learning first, we need to understand a few basic concepts. One of the basic concepts is Activation Function. In my next article, I’ll try to explain in details what activation function is & why we need them in a neural network. But if you want to learn more about neural networks right now then below I’ve shared some resources for you.

• Python Deep Learning From Scratch This is a Bangla book and it’s written by Rokibul Hassan. He is the best Bangla teacher or content creator when it comes to deep learning and machine learning. I have started learning deep learning after reading this book.
• Krish Naik’s Deep Learning Youtube Series
• Code Basics’s Deep Learning Youtube Series
   
   

Thanks for reading this article. Hope you will come back to read the next article on the Activation Function